√100以上 一次 関数 やり方 342853-一次関数 やり方

 一次関数の問題の解き方 パターン1～3文章から一次関数の式を求める パターン1 直線 y＝3x y ＝ 3 x に平行で点 (0,−2) ( 0, − 2) を通る直線の式を求めよ。 一次関数において平行な直線は傾きが等しいということを指すので、「直線 y＝3x y ＝ 3 x に平行」というのは「傾きが3」ということです。 そして「点 (0,−2) ( 0, − 2) を通る」というのは「切片が2」ということ。 つ 中学2年生の山場の一つである一次関数。 うまく理解できれば、3年生の二次関数も楽々クリアできます。 受験でもよく出題されるので、マスターしておきたいところですね。 初めて一次関数を教える場合は、以下のシナリオに沿って教えると、理解してもらいやすいです。一次関数 式の求め方グラフが平行になる （7）点 (－2,10)を通り、直線 に平行である直線 2直線が平行になるというのは 2直線の傾きが等しくなるということです。 つまり 『 に平行』というヒントから傾きが－2になるということが読み取れます。 そうすると、この問題は 点 (－2,10)を通り、傾きが－2である直線の式を求めなさい。 と同じことです。 パターンで言えば、（2）と同じですね。

一次関数の問題の解き方 7パターン 数学fun

一次関数 やり方

一次関数 やり方- 一次関数の練習問題 上記のことをふまえて、一次関数の問題を解いてみましょう。 問題 （1）一次関数y=2x3の傾きとy切片を答えよ。 （2）2つの座標A（0,1）、B（4,9）を通る直線の式を求めよ。 （3）y=5xに平行で、座標（1,8）を通る直線の式を求めよ。 解答このように、関数では 「代入」すれば答えを出せる問題がとても多い です。 関数の問題の特徴として覚えておくといいですね。 何を使って勉強すればいい？ 一次関数や二次関数に限らず、 苦手な単元は学校の基本教材から勉強しましょう。

1

 1 分数関数の積分に必要な知識 冒頭でも述べましたが、分数関数の積分は、体系立てて説明されているものがなくて、なんだかごちゃごちゃしていて難解なもののようなイメージを持ちがちです。 しかし実際は、とても簡単です。 実のところ必要な知識 中2 一次関数1 (グラフの書き方) 今回から、数学講座を始めたいと思います。 なるべく綺麗にカテ分けしますので、続けてご覧いただきやすいようにしますね。 第1回の今回は一次関数についてお話していきます。 本日はグラフの書き方から行きましょう一次関数 一次関数正方形になる座標の求め方をイチから！ 今回は中2で学習する一次関数の単元からちょっと発展的な 「正方形になる座標」 について取り上げます。 一次関数の応用をマスターしたい方にぴったりの問題となっているので、まずは例題をチェックして演習問題にチャレンジしていきましょう ('ω')ノ 今回の問題はこちらの動画でも解説しています。 動画の方が伝わりやすい部分も

 一次方程式（分数）の解き方例題① 次の方程式を解きなさい。 かず先生 上で紹介したように、分数を消そう。 分母にある3を両辺に掛けるよ！ ポイントとしては、分数ではない数にもちゃんと3を掛けるということ。 これを忘れないようにしてくださいね！ 一次方程式（分数）の解き方例題② 次の方程式を解きなさい。 ゆい あれ？ 分母の数が違うけど こういう場合は何を掛中2数学。「y = 2x 3」のグラフをかきなさい。うわ「1次関数のグラフ」、かき方が分からん（ガクッ）おや、中学生が倒れそう。立て、立つんだトォォォォ～ッ！ オール5家庭教師、見参ッ！ グラフなんて一瞬でかける！ コツを無料公開だ。 一次関数は「y = 4x」のようにxが一つの場合の関数のことです。 ＜例＞ y＝5x＋4 → 一次関数 y＝4＋2x → 一次関数 y＝23 → 一次関数ではない y＝2x² → 二次関数 y=2x²のようにxが2乗であれば二次関数になるし、xが3乗あれば三次関数って呼ばれます。 つまり、式の中のxが2乗でも3乗でもなくただのxであれば一次関数ということです。 今からやっていく一次関数は、xが一つ

「一次関数の利用の問題について、解き方のコツ」を紹介します。 コツ→3つのパターン 一次関数の利用の問題で最も重要なのは、どの値を「x」「y」とおくかです。 これを間違えなければ、正解にたどり着くことができます。 コツのポイントを3つのパターンに分けて説明します。 パターン1「文中にxとyがでてくる問題」 1つ目は問題文の中に、何をx、yとおいたらいいのか？ が書いてある 中学 2 年生の 2 学期では「一次関数」、「平行と合同」、「三角形の性質」あたりを習いますが、9月～ 10 月ごろは「一次関数」がメインの単元となります。 ザックリ言うと、 一次関数とは「 y=axb の形をした式」 のこと、という捉え方で概ね大丈夫です。 この一次関数で何より大切 関数の基本は、たとえば 一次関数ではy＝axb 二次関数ではy＝ax2 のような関係式がありますが これにx＝3 y＝6のような数値を代入してaの値を求めるというような問題が基本問題として問われます。 このやり方は、実はどんな関数でも同じです。 要は「代入」すれば、ほとんどの基本問題は出来てしまうのです。 比例でも反比例でも 一次関数でも二次関数でも三次関数でも すべて

一次関数とは 式の求め方や一次関数の利用問題の解き方 受験辞典

一次関数の変化の割合を求めたい時 Xの増加量分のyの増加量で解きたい 右 Yahoo 知恵袋

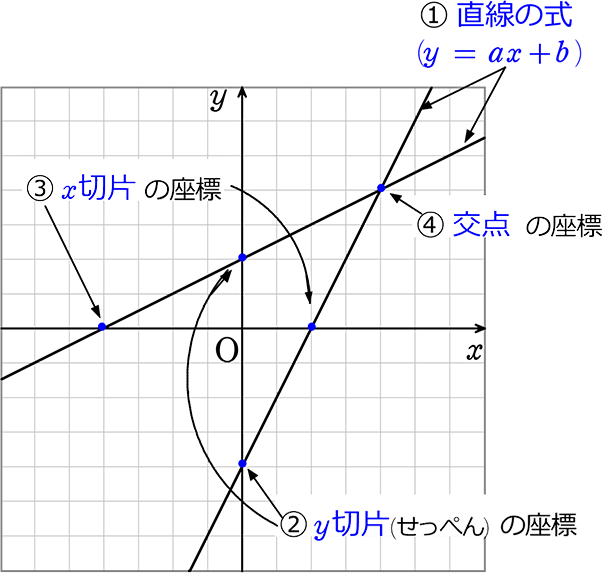
 一次関数の直線の式がわかる3つの求め方 まず、直線の式が計算できるケースを確認しよう。 つぎの4つの要素のうち、2つの値がわかっているときに式が求められるんだ。 傾き（変化の割合） 切片 直線が通る座標1 直線が通る座標2 たとえば、傾きと切片がわかっているとき、とか、座標と切片がわかっているとき、みたいな感じだね^^ 求め方のパターンをみていこう！ パターン1 「1次関数の式の出し方は大きく分けて 2通り 。 ・傾きと1点から出す方法。 ・2点から出す方法。 傾きと1点から1次関数の式を出す y = axb の傾きaとx, yに数字を代入してbを求める。 例傾き3で、x=1のときy=−2となる1次関数の式を求める。 傾きa=3 なので、 y=3xb この式に x=1, y=−2を 代入 してbを出す。 2 = 3×1b b = 32 b = −5 よって y = 3x −5 となる。 確認 次の条件にあて 今回は1次関数に絞りますが、他の関数でもやり方は同じです。 1次関数の式の求め方は4パターン です。 出題された問題がどのパターンにあてはまるのかわかるようになると問題をすんなりと解くことができるようになります。

グラフの平行移動とは 二次関数などの公式と作図を解説 受験辞典

一次関数と二次方程式の合わさった問題なんですけど 下の画像の問題を教えて下さい アンサーズ

 ここでは、一次関数の式の求め方を問題のタイプ別に説明していきます。 求め方① 傾きと切片から求める 問題文やグラフに隠れている傾き と切片 を読み取る問題です。 例題① 問題文から読み取る場合 例題① 直線 に平行で、切片が の直線の式を求めよ。 問題文から、傾きの情報を読み取ります。 解答 傾きが の直線に平行であるから、求める直線の傾き は また、切片 より 求める直線中学生の勉強方法 中2数学一次関数ってなに？ 比例とどう違うのか、解説します！ こんにちは、あすなろスタッフのカワイです。 本記事では、中学1年生の頃に勉強した「比例」の考えを拡張した「1次関数」という単元の触りについて解説していき 11/9/10 1011 2 回答 ワードかエクセルで1次関数のグラフの書き方について教えてください。 ちなみに、Microsoft Office Excel 07 Microsoft Office Word 07 です。 パソコン弱い私でもわかるように、どなたかお願いします。 たとえば、 y＝2x＋3 のグラフをつくりたいです。 Word ・ 14,4 閲覧 ・ xmlns="http//wwww3org/00/svg"> 500 ベストアンサー har******** さん

一次関数 式の求め方をパターン別に問題解説 数スタ

数学 中3 41 二次関数の利用 一次関数とのコラボ編 Youtube

 一次関数のグラフはとても単純でした。 直線が、斜めに走っているだけです。 そのため、二次関数のグラフは、一次関数のグラフとはまるで別物のように感じる人も少なくありません。 しかしグラフも「 二次関数は一次関数から 1 つ増えただけ 」です。 一次方程式の解き方手順 文字は左辺に、数は右辺に移項する それぞれを計算して、 の形にする の係数で両辺を割る 完成！ 余裕があるときは、解を代入して確かめる かっこがある場合 ⇒ まずは、かっこをはずす！ 小数がある場合 ⇒ 両辺を10倍、100 一次関数のグラフ書き方 式から傾きと切片を読み取る 切片の点をとる 傾きから点をとる ②③の点を線で結ぶ 完成！ では、これらの手順にそって一次関数のグラフを書いてみましょう。 次の一次関数のグラフをかきなさい。 まずは、式から傾きと切片を読み取ります。 すると、傾き 、切片 ということがわかりますね。 次に、 軸上に切片 の点を取ります。 次に傾きをみましょう。 傾き

一次関数の動点の問題で この問題は解説をみながらやったのですがやり方や意 Yahoo 知恵袋

数学 中2 41 一次関数の利用 ばねとろうそく編 Youtube

 今回は一次関数の問題です。 一つ気付いたんですが、面白い数学の問題の問題が最近ただの中学数学になってますよね？ お勉強のカテゴリーあるの忘れてまして、次からはここに記事を載せていこうと思います。 自分的には面白い問題のつもりでしたがそれでは関数を作り方をみていきます。 戻り値の型 関数名 (引数) { 処理; 一次関数とはずばり、 y = ax b という形をした関数のことさ。 もう少しわかりやすく説明すると、 xが1回以下だけかけられた関数のこと なんだ。 yの右側がxの 一次式 ならそいつは一次関数ってわけさ。 たとえば、 y = 9x とか、 y = 9000x 100 が一次関数になるよ。 だって、y = ax bの形になっているし、xの項はすべて1次式だからね。 これさえ覚えておけば大丈夫。 一次関数

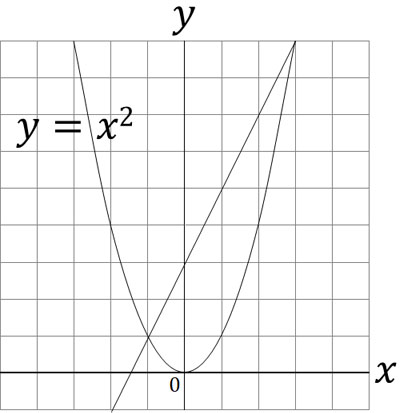
中学数学の二次関数 問題の解き方の基本とグラフの書き方 Hatsudy 総合学習サイト

中2数学 １次関数のグラフの書き方 例題編 映像授業のtry It トライイット

まず、一次関数とは、y = ax b という式で表されるものです。 これをエクセル上で表し、グラフにしていきましょう。 今回はy=5x2という一次方程式を描いていきましょう。 まずは、xの値を1刻みで入力していきます。 続いて、一次関数のyの値を求めていきます。 セルに＝5*（xのセル）2と入れます。 Enterキーで一次関数の計算を確定させていきます。 オートフィル機能の意味と使い方 （ベクトルの一次結合 a → 、 b → という2つのベクトルに対して、それぞれを定数倍して足し合わせた p a → q b → という形のベクトルを、 a → と b → の一次結合と言います。 例えば、 a → = ( 1 0) 、 b → = ( 0 1) のとき、 ( 3 2) = 3 a → 2 b → と書くこと一次関数の解き方：傾き・切片でのグラフの書き方、交点の求め方 中学数学 中学数学で比例や反比例の定義と概念を学んだあと、次に勉強するのが一次関数です。 比例のグラフと似ており、\ (x\)の値が増えるに従って\ (y\)の値が一定割合で増えるのが一次関数です。 一次関数では、傾きと切片という考え方があります。 どのような傾きになっており、切片となっているのかによってグラフの形が変

B8ou3tedn Daym

中学数学 一次関数とはなんだろう Qikeru 学びを楽しくわかりやすく

一次関数 （5,7）を通りy軸に平行な直線の式を求めるやり方を教えてください 中3数学平方根の章末問題です。 画像の2問の解き方の過程を教えてほしいです。 一次方程式の計算を行うには関数は必要なく、そのままの数式を入力すればいいです。 今回では、出力したいセルに ＝2*5 と入れます。 ENTERにて処理を確定後、オートフィル（セルの右下に出る十字をダブルクリック）し、一括で一次関数のyの数値を求めます。 このようにして一次方程式のyの数値の計算ができました。 一次方程式（一次関数）の解（x）を求める 続いて一次方 一次関数が苦手な原因 ここからは、 一次関数が苦手な原因 についてお伝えします。 まぁどれかだと思います。 どれだったとしても、 ここでお伝えするやり方で練習すれば、 出来るようになると思うので 心配ありません。 一次関数が苦手な原因① 教える人が下手

一次関数とは 式の求め方や一次関数の利用問題の解き方 受験辞典

S7rthoilhqumbm

 一次関数の基本 最初に少しだけ一次関数の基本に触れておきます。 一次関数の ＝ ＋b y ＝ a x ＋ b で、 a は傾き、 b b が切片を表します。 一次関数の場合、傾きと変化の割合は同じです。 変化の割合だけを求める問題も多くありますから、こちらの記事も参考にされてください。 >> 一次関数の変化の割合の求め方一次関数とは、「一次の関数」、つまり「含まれる文字の次数が1の関数」を指します。 比例も一次関数の一種ですが、比例の式に "定数項" が加わったものが一次関数です。 一次関数を表す式： 『y＝ax b y ＝ a x b 』 a a 傾き（グラフにした時の直線 これが、導関数の定義に従った微分のやり方です。 しかし、関数を微分するたびに定義どおりの計算を行うのは大変ですよね。 そこで、次に示すやり方②のように 微分の法則性をまとめた公式 を使うことで、計算を省略することができます。 ② 微分公式を使って微分する 次に、微分公式を使った微分のやり方です。 例題 次の関数を微分せよ。 先ほどと同じ例題ですが、微分公式を使う

１次関数の値の変化 増加量と変化の割合 教遊者

一次関数の問題の解き方 7パターン 数学fun

 一次関数に作図の問題が必ず出るように、 グラフから式を求める問題も必ず出ます！！ 問題の3～7に関しては60点以上を取りたい生徒は必ずやって下さい！！ ポイントとしては、5、7の問題は連立方程式を使って解くやり方をオススメします☆ 一次関数の利用 動点の問題 図形の中で点が動き、面積などをxとyの一次関数で表す問題です。 解き方のポイント ＊長方形や三角形の辺上を動くとき。それぞれの辺上で面積がどうなるかを考えましょう。 例）①辺AB上を動くとき ②辺BC上を動くとき ③辺C1次関数基礎1 1 次の問いに答えよ。 (1)1次関数でxが2から3まで変化したときにyは5から7まで変化した。変化の割合を求めよ。 (2)1次関数でxが3から7まで変化するときにyが2から–6まで変化した。変化の割合を求めよ。 (3)y=–2x3について 変化の割合を求めよ。

一次関数とは 式の求め方や一次関数の利用問題の解き方 受験辞典

一次関数の問題の解き方 7パターン 数学fun

 OrderSelect関数の基本的な書き方を解説しましたが、ここからは具体的な使い方について解説していきます。 OrderSelect関数はポジションを1つだけ選択する関数なので、 for文 を使って全てのポジションを選択する方法がよく使われます。} 関数はこのように「戻り値の型」「関数名」「引数」を指定して作成します。 関数に int型の戻り値がある場合

3分で誰でもわかる 平行移動の公式とやり方を見やすい図で解説します 高校生向け受験応援メディア 受験のミカタ

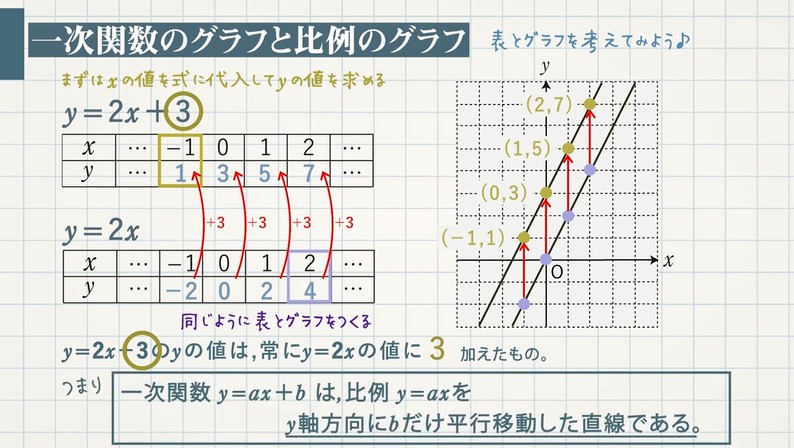
一次関数とグラフ Y Ax B 教遊者

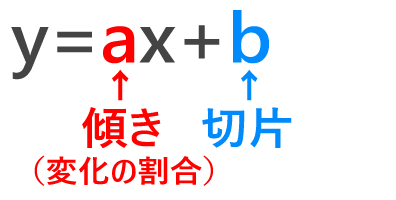
傾きと切片の求め方 一次関数ｙ ａｘ ｂのａとｂに注目だ 中学や高校の数学の計算問題

数学 中2 36 一次関数の交点をだす 基本編 Youtube

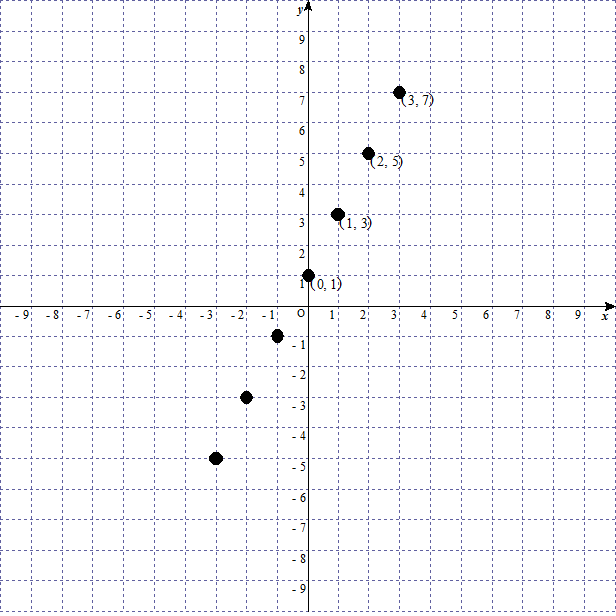
一次関数のグラフの書き方 プロットのやり方 切片と傾きの意味 Irohabook

一次関数のグラフ 無料で使える中学学習プリント

ｙ ａｘ2の変化の割合の求め方 基本と裏ワザ 現役塾講師のわかりやすい中学数学の解き方

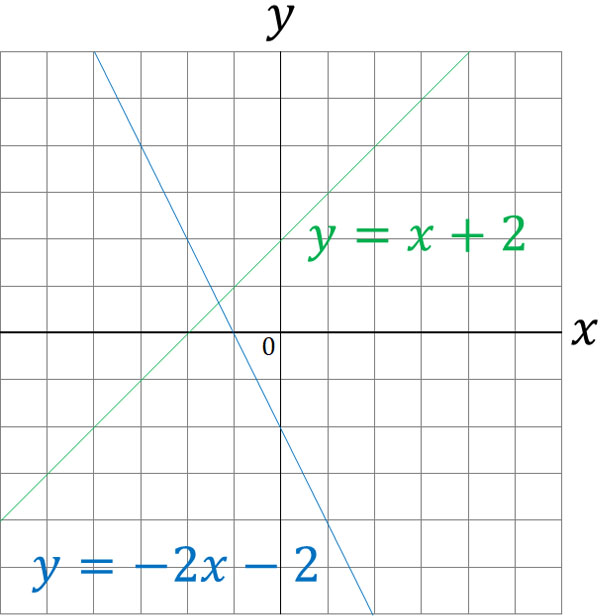
一次関数の解き方 傾き 切片でのグラフの書き方 交点の求め方 Hatsudy 総合学習サイト

一次関数のグラフ 無料で使える中学学習プリント

一次 関数 と 方程式 ニスヌーピー 壁紙

1

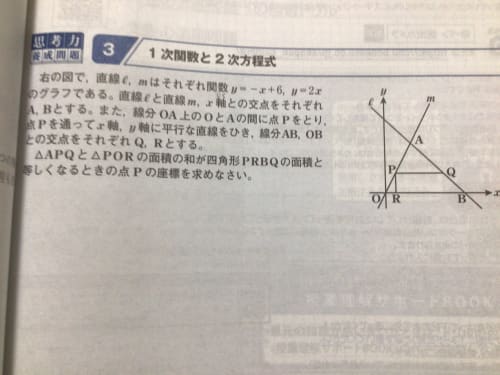
一次関数と二次方程式の合わさった問題なんですけど 下の画像の問題を教えて下さい アンサーズ

中学２年数学練習問題 一次関数の利用 距離 料金等の文章題解答

9 3 １次関数 面積 勉強できようサイト

Abryvbxom7yvnm

一次関数の解き方 傾き 切片でのグラフの書き方 交点の求め方 Hatsudy 総合学習サイト

いえがくサポート 9月 16

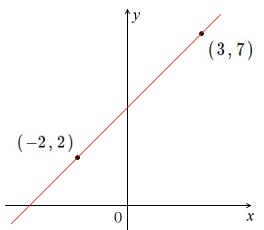
1次関数の交点の座標とグラフから直線の方程式を求める方法

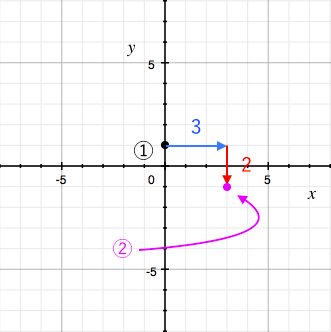
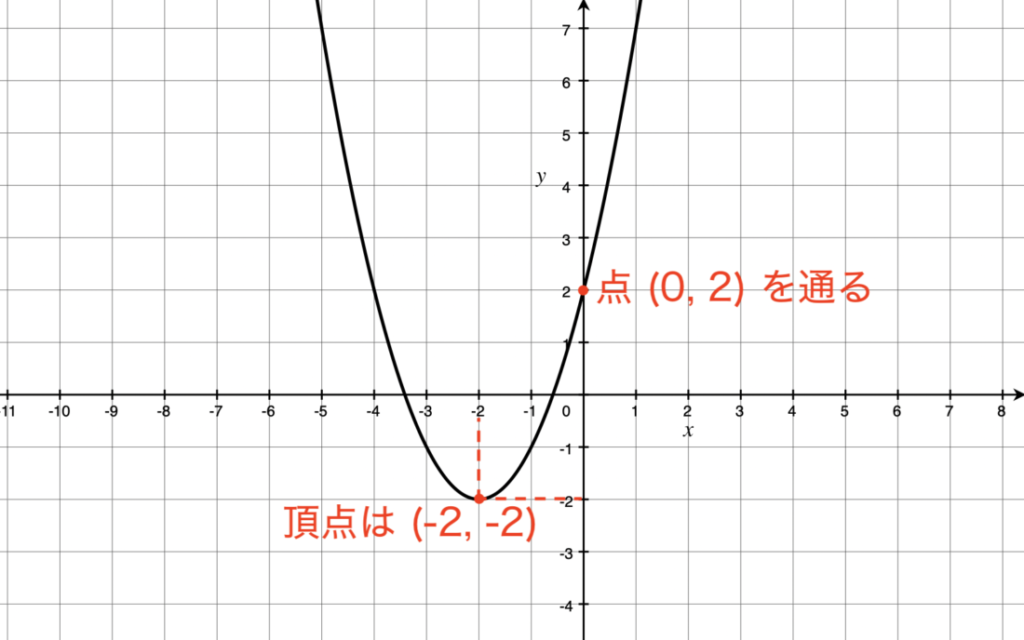
二次方程式 平方完成 X M 2 Nへ変形 苦手な数学を簡単に

中学1年数学 一次方程式 一次方程式の解き方 移項の本当の意味を理解すれば全部解ける 数学の面白いこと 役に立つことをまとめたサイト

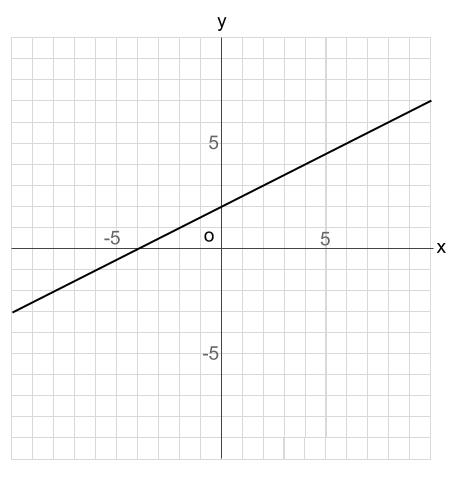
中学数学 1次関数 グラフの読み取り 中学数学の無料オンライン学習サイトchu Su

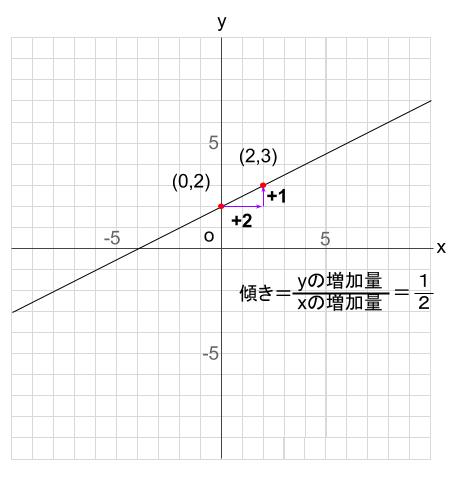
中学数学 1次関数 グラフの読み取り 中学数学の無料オンライン学習サイトchu Su

3分で分かる 一次関数の意味 用語 グラフの書き方をわかりやすく 合格サプリ

切片とは 超簡単 切片を一瞬で求める方法 傾きとの違い 高校生向け受験応援メディア 受験のミカタ

一次関数を子供に教える

割引クーポン 三澤の数学 一次関数とテキストセット 参考書 Ssfltt Com

一次関数を子供に教える

中学数学 一次関数

二次関数のグラフの書き方とグラフの問題を一気に紹介 スタディクラブ情報局

1

１次関数の値の変化 増加量と変化の割合 教遊者

中2の数学 をバッチリ攻略 連立方程式や一次関数を解説 家庭教師ジャニアス

中学数学 一次関数

1

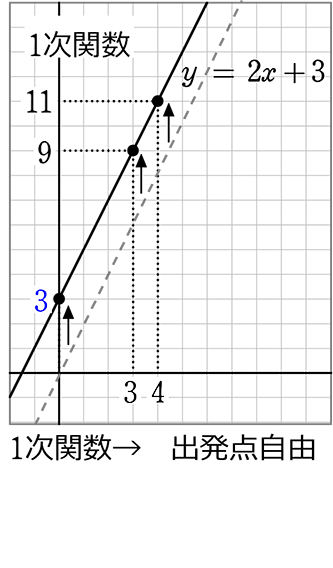
中学数学 一次関数

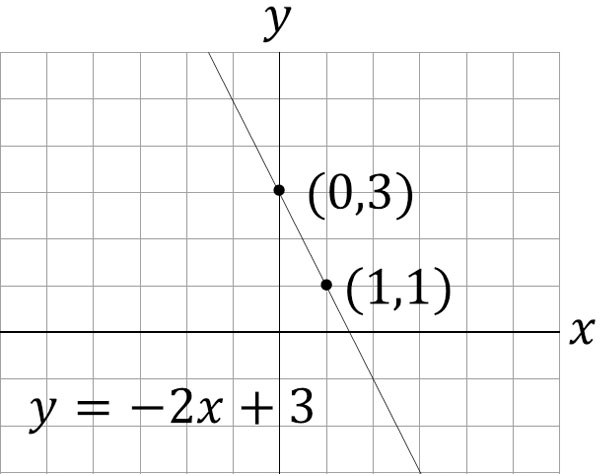
一次関数の解き方 傾き 切片でのグラフの書き方 交点の求め方 Hatsudy 総合学習サイト

Download 中学数学 たすき掛け因数分解のやり方 Images For Free

一次関数の解き方なのですがなぜこの答えになるのかを教えて下さい を変形 Yahoo 知恵袋

一次関数の問題の解き方 7パターン 数学fun

一次関数の利用ー速さ 無料で使える中学学習プリント

速さと一次関数の問題 去年の今日日記 都立入試の情報満載 こじんまりしたこじま塾ブログ

Mathematics １次関数 ６ 応用問題の解き方 １ １次関数と図形 働きアリ

一次関数のグラフの書き方を超わかりやすく解説 受験辞典

一次関数とは 式の求め方や一次関数の利用問題の解き方 受験辞典

1

中2一次関数 中2の息子が明日 期末テストなので数学の一次関数を 質問さ Okwave

数学 中2 42 一次関数の利用 一人のみはじ編 Youtube

中２数学 一次関数の 切片 の意味 その２ 小中５科目のミラクル解説 ミラクル解説 塾のあすみが丘プロダクティブは 学力に合わせた個別指導塾

一次関数y 2分の1ｘ 3について答えなさいとの事です Clearnote

完全版 一次関数のグラフから利用問題まで解き方まとめ 中学数学 理科の学習まとめサイト

一次関数と反比例の融合問題の解き方を解説 数スタ

次の一次関数で傾きが3分の2で X軸との交点のx座標が 6をの式の求め方 中学校 教えて Goo

一次関数 グラフの書き方 切片が分数のときにはどうする Youtube

一次関数 表から式を求めるやり方についてイチから解説 Youtube

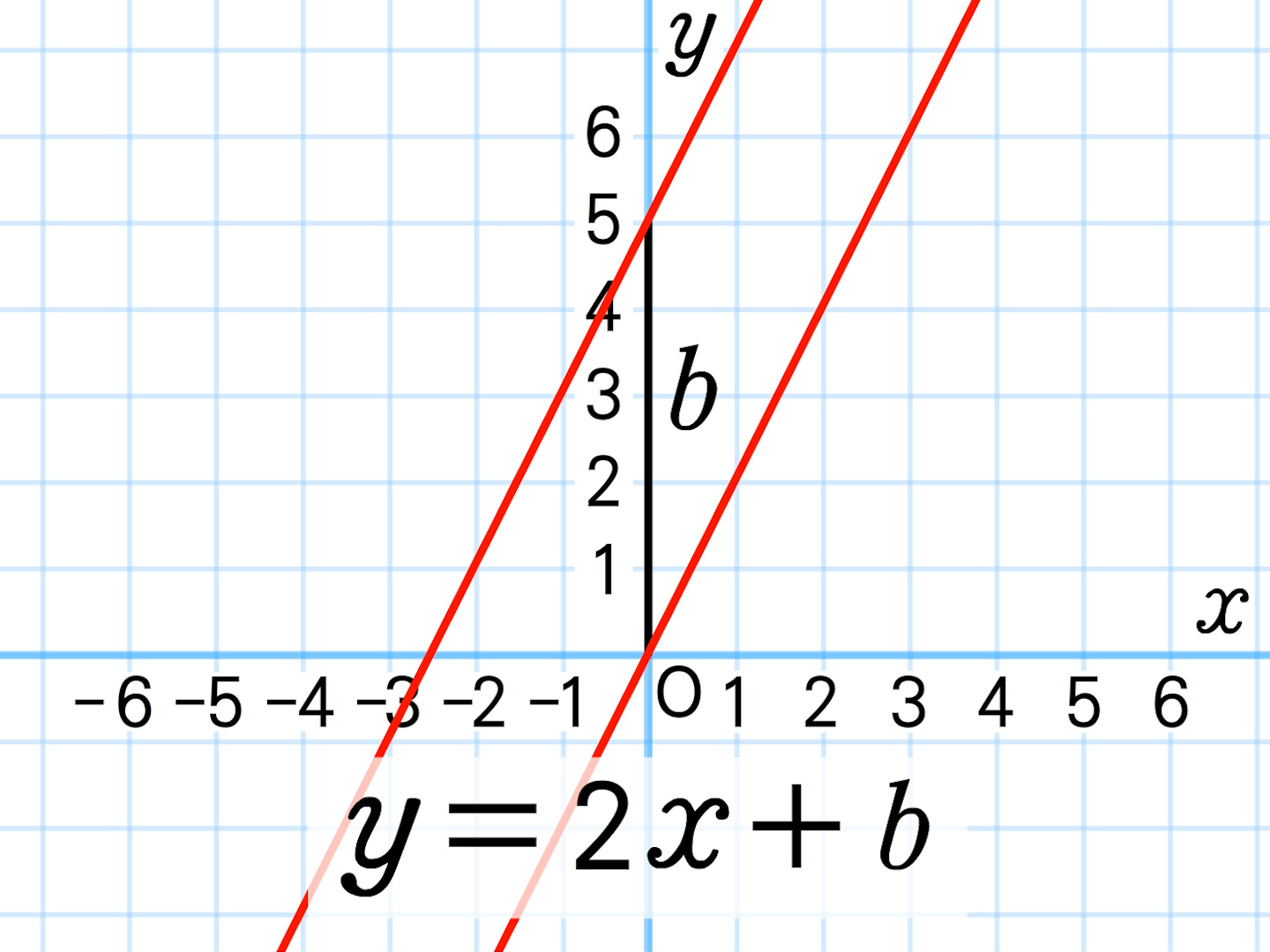
2年 １次関数のグラフ １ 数学イメージ動画集 大日本図書

一次関数のグラフを見て 傾きと切片を１０秒以内に求めよう 中学や高校の数学の計算問題

9 1 １次関数 グラフの描き方 読み取り方 勉強できようサイト

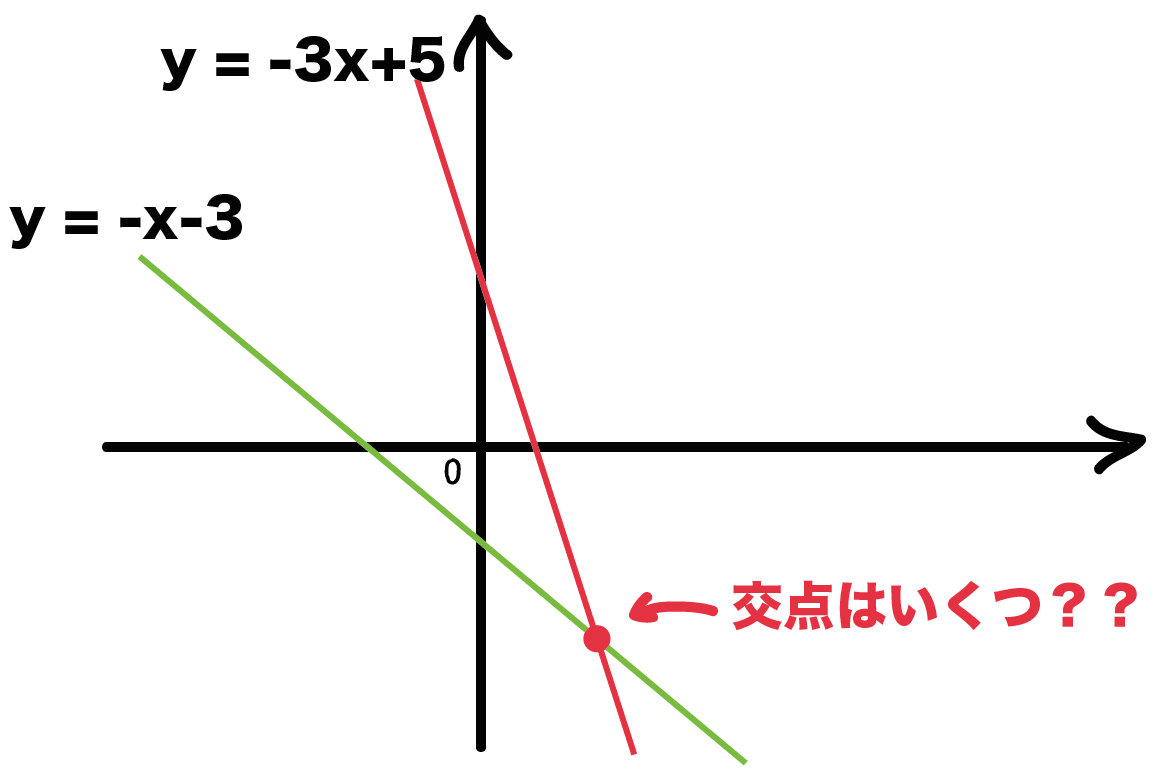
2直線の交点の座標の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

数学 中2 32 一次関数の式をもとめる 基本編 Youtube

一次関数のグラフがスラスラ書ける 見やすい図で徹底解説 高校生向け受験応援メディア 受験のミカタ

動点 一次関数の人気動画を探索しましょう Tiktok

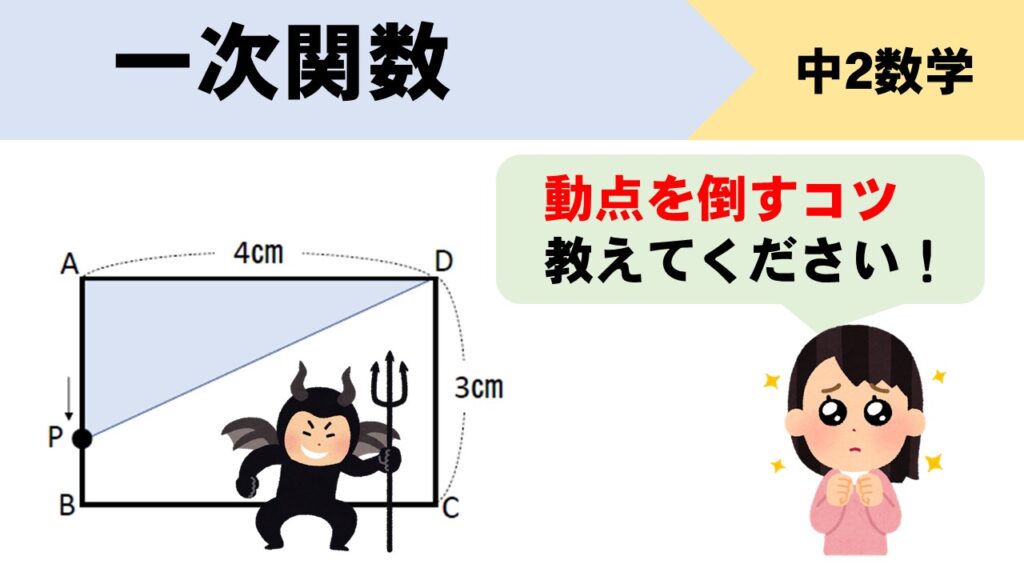
1次関数 みんなニガテな動点の問題のコツを伝授 数スタ

2

中学数学 一次関数

至急中2の数学の一次関数の問題です X 3y 3の時のxとyの解き方と答 Yahoo 知恵袋

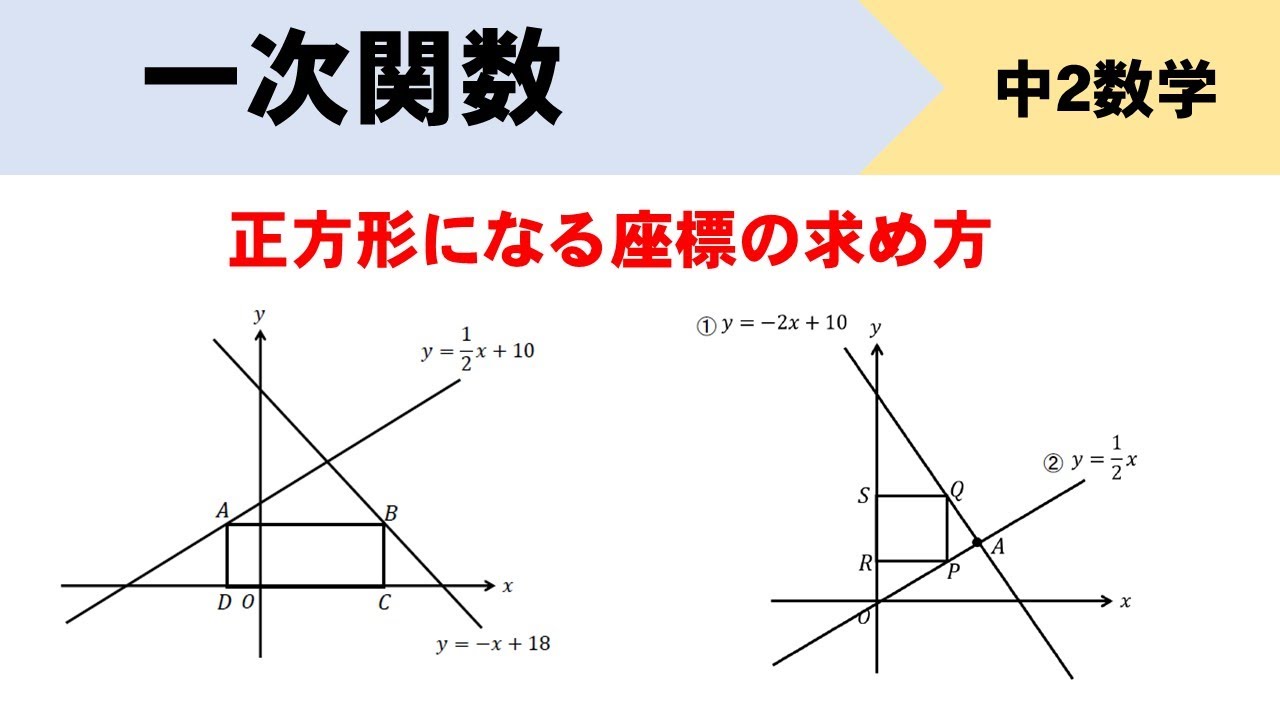
一次関数 正方形になる座標の求め方をイチから 数スタ

一次関数とは 式の求め方や一次関数の利用問題の解き方 受験辞典

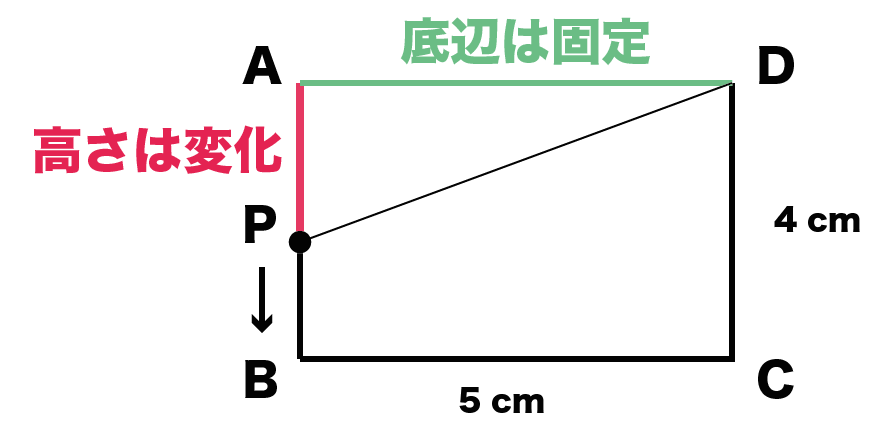
一次関数の利用 動点の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

一次関数の応用問題の解き方がわかりません 弟の数学の宿題を手伝っ 数学 教えて Goo

中学数学 一次関数

一次関数のグラフ問題の解き方が知りたいです 四角形abcdが平行四辺形 Yahoo 知恵袋

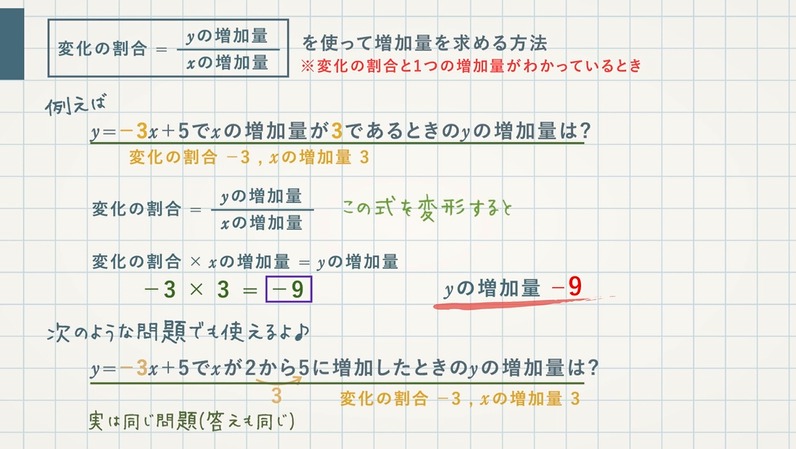
１次関数の値の変化 増加量と変化の割合 教遊者

中学の一次関数 ２次関数の勉強のコツを知って得意になろう

Mathematics １次関数 ６ 応用問題の解き方 １ １次関数と図形 働きアリ

中学数学 1次関数と2次関数y Ax2のグラフの3つの違い Qikeru 学びを楽しくわかりやすく

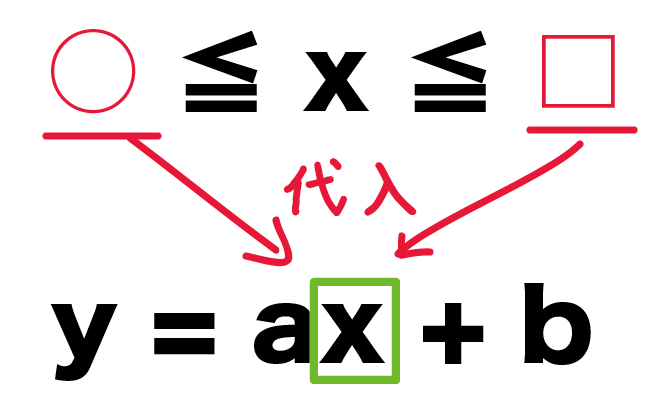
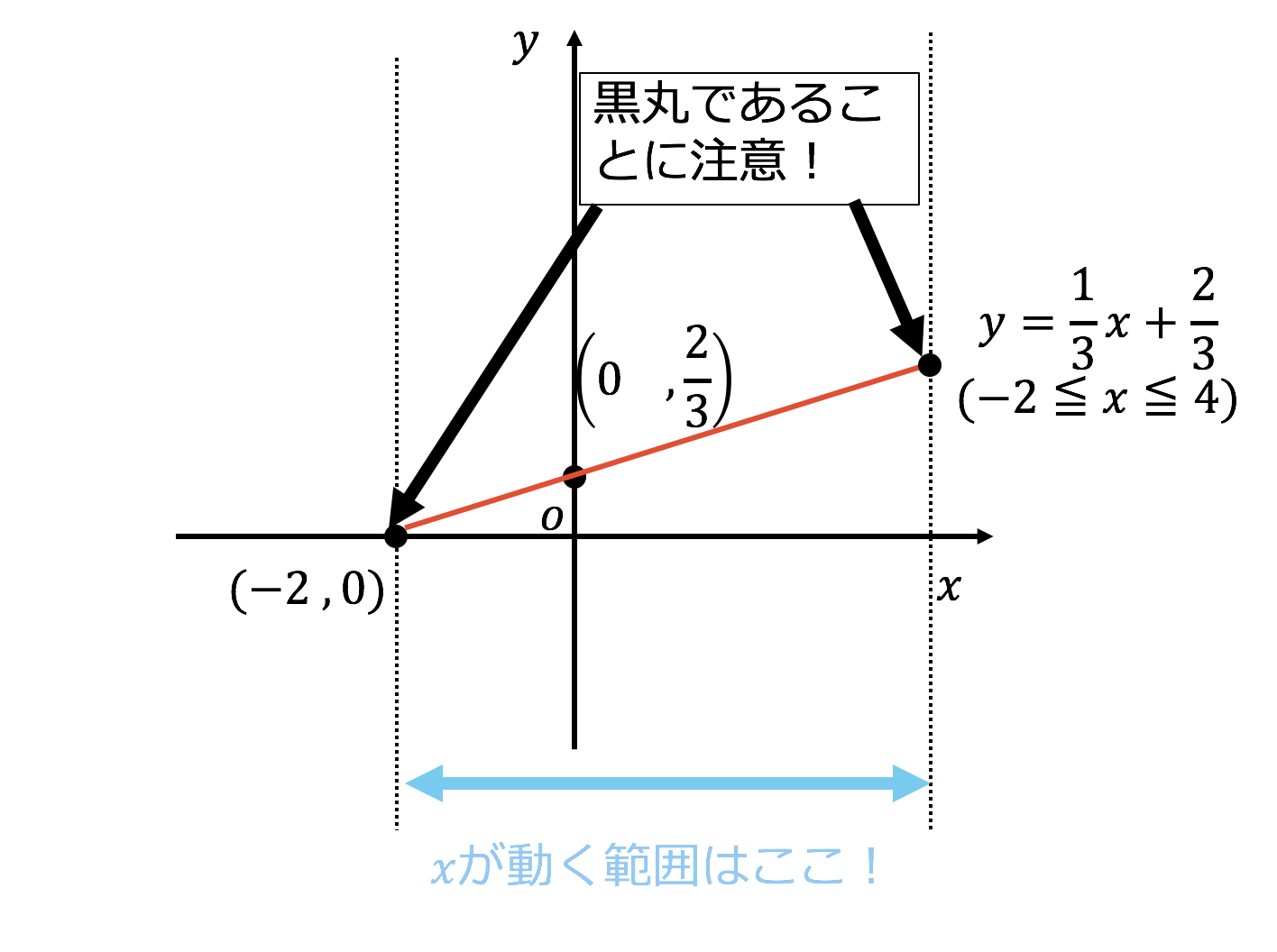
一次関数 X Yの変域の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく

一次関数の問題がわかりません 次の方程式のグラフをかきな Yahoo 知恵袋

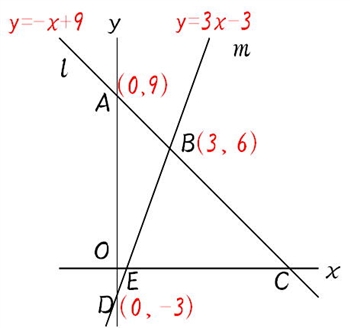
中学の一次関数 ２次関数の勉強のコツを知って得意になろう

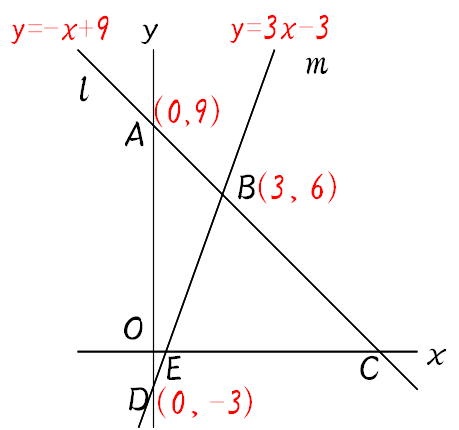
Mathematics １次関数 ６ 応用問題の解き方 １ １次関数と図形 働きアリ

一次関数の人気動画を探索しましょう Tiktok

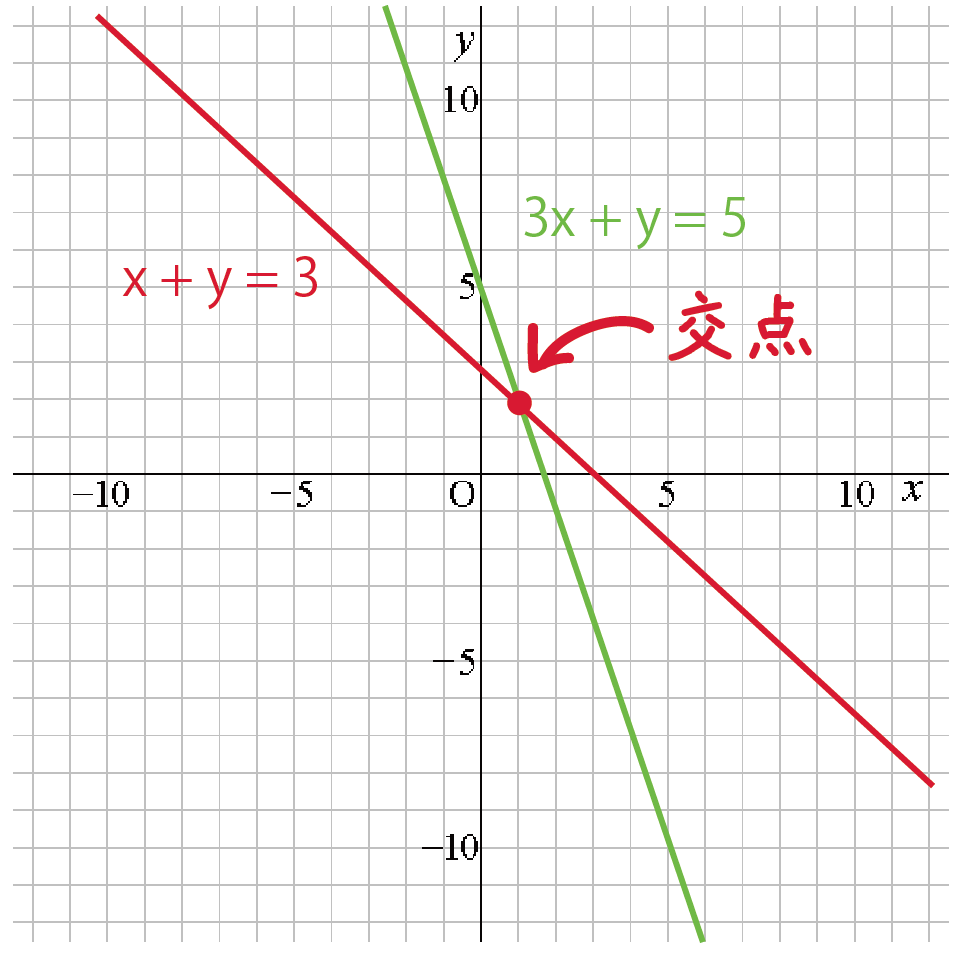
一次関数 グラフから連立方程式の解を求める3つのステップ Qikeru 学びを楽しくわかりやすく

一次関数 裏技の人気動画を探索しましょう Tiktok

一次関数 二元一次方程式をグラフにする2つの書き方 Qikeru 学びを楽しくわかりやすく

一次方程式の解の求め方 数学fun

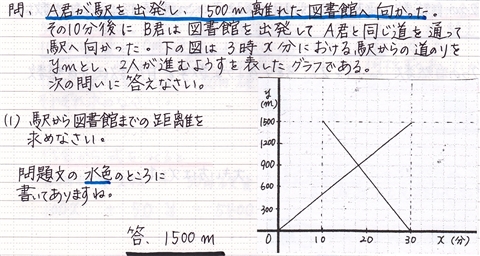
中学の一次関数 ２次関数の勉強のコツを知って得意になろう

3分で誰でもわかる 平行移動の公式とやり方を見やすい図で解説します 高校生向け受験応援メディア 受験のミカタ

Incoming Term: 一次関数 やり方,